Prethodno poglavlje | Pocetna strana | Sledece poglavlje

 

 

2. GEOMETRIJA I KINEMATIKA MEHANIZMA ROBOTA

 

Razmatraćemo probleme geometrije mehanizma robota, i na početku dati kratak pregled sadržaja glave. Kako je mehanička struktura robota, u stvari, je­dan zglobni mehanizam, to ćemo najpre definisati i objasniti neophodne pojmove iz teorije mehanizama. Zatim ćemo definisati geometriju manipulacionih robota a posebno ćemo obraditi slučajeve koji se javljaju u praktičnim realizacijama. U ok­viru izlaganja o kinematici govorićemo o brzini i ubrzanju u zglobovima mehanizma i pokazali vezu sa tzv. korisnom brzinom prenošenja radnog predmeta.

 

Tokom razmatranja kinematike najviše ćemo se baviti pitanjem određivanja položaja i kretanja robota preko takozvanih unutrašnjih i spoljašnjih koordinata. Tu se obraduje i način preračunavanja kretanja iz jednih koordinata u druge, od­nosno direktni i inverzni problem kinematike robota.

 

2.1. OSNOVNI STAVOVI IZ TEORIJE MEHANIZAMA

 

Teorija mehanizama kao oblast nauke i tehnike proučava sisteme tela među­sobno povezanih raznim tipovima veza. Iz ove veoma široke oblasti izvući ćemo one pojmove koji su bitni za proučavanje robotike. Pri tome, zadržaćemo određeni nivo strogosti u definicijama tih pojmova, a istovremeno ćemo se rukovoditi time da objašnjenja budu što jednostavnija i jasnija. Prvo, potrebno je proučiti tipove veza tela koja obrazuju mehanizam, a zatim različite strukture mehanizama koji se javljaju u robotici.

 

2.1.1. Kinematički parovi

 

Kinematički par podrazumeva dva međusobno povezana tela. U zavisnosti od načina vezivanja ta dva dela, kinematičke parove delimo na određene klase. Da bismo te klase mogli definisati razmotrićemo moguće načine veze dva tela.

 

Posmatraćemo prvo jedno slobodno telo. Ono može da se kreće na šest ne­zavisnih različitih načina: može da se kreće translatorno duž osa x, y, z i može da se obrće oko svake od tih osa (vidi sliku 2.1), dakle ima tri moguće, odnosno slobodne translacije i tri slobodne rotacije. Iz toga zaključujemo da je potrebno šest veličina (koristićemo izraz parametri) da bi se jednoznačno odredio položaj tela: tri parametra da bi se odredilo translatorno kretanje i tri da bi se odredilo rotaciono kretanje, odnosno orijentacija tela.

 

 

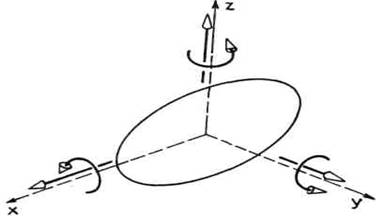
Sl.2.1.Moguća kretanja slobodnog tela

 

Broj stepeni slobode je broj slobodnih (odnosno mogućih) ne­zavisnih kretanja, ili drugačije rečeno, to je broj nezavisnih parametara koji su potrebni da bi se jednoznačno odredio položaj tela. Posmatrajmo sada dva tela, valjak i klešta, međusobno vezana na način kako je to pokazano na slici 2.2. Valjak, u odnosu na klešta ima dve slobodne transla-cije (duž x i y ose) i dve slo­bodne rotacije (oko x i z ose), dakle postoje ukupno 4 slobodna međusobna kretanja ova dva tela. Zato kažemo da ovaj kinematicki par ima 4 stepena slobode. U ta­beli na slici 2.3 dati su neki slučajevi kinematickih parova, njihova moguća kretanja, broj stepeni slobode i klasa kinematičkog para.

 

Za primenu u robotici najvažniji su kinematički parovi pete klase. Kine­maticki par pete klase koji dozvoljava samo jednu rotaciju zvaćemo rotacionim pa­rom ili rotacionim zglobom, a par koji dozvoljava samo jednu translaciju zvaćemo translatornim parom ili translatornim zglobom. Te parove ćemo shematski crtati kao na slici 2.4.

 

 

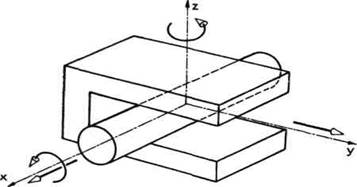
Sl. 2.2. Primer kinematičkog para sa 4 stepena slobode

 

Pored parova pete klase, u teoriji robotike koriste se i drugi parovi, ali o njima će biti reči kasnije.

 

 

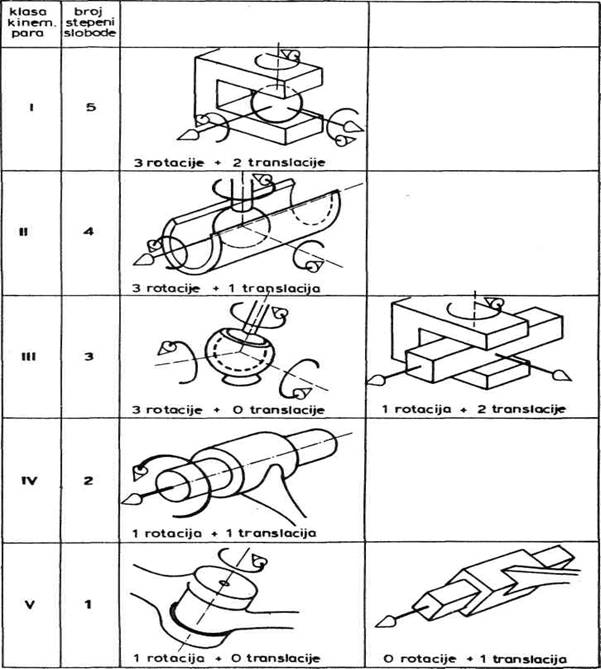
Sl. 2.3. Izgled kinematičkih parova

 

 

 

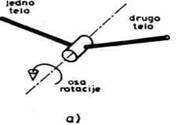
Sl. 2.4. Rotacioni (a) i translatorni (b) zglob

 

 

 

 

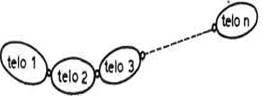
Sl. 2.5. Lančani sistem tela     

 

2.1.2.Kinematički lanci

 

Nizove tela povezanih kinematičkim parovima nazivamo kinematičkim lancima.Ovde će­mo podrazumevati da su veze ob­lika rotacionih ili translatornih zg­lobova. Shematski, kružić  između dva predstavlja bilo koji od zglobova (sl.2.5.).Složeniji zglobvi razlažu se na zglobove pete klase između kojih se nalaze kratki segmenti.         

 

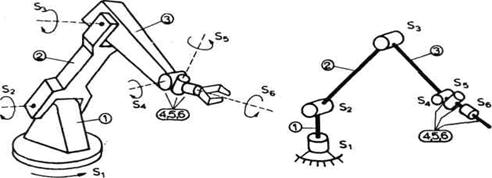
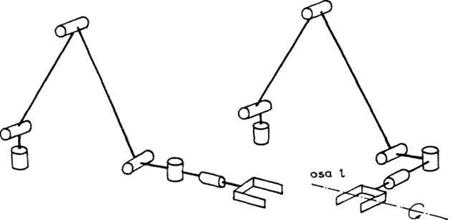
Kinematički lanci su posebno važni u robotici zato što mehanizam svakog robota predstavlja, u stvari, jedan kinematički lanac. Na slici 2.6 predstavljeno je nekoliko manipulacionih robota i shematski su prikazani odgovarajući kinematički lanci.

 

Svako telo, elemenat lanca, nazivaćemo segmentom lanca. Segmente lanca smatramo krutim, nedeformabilnim telima. Lanac se, dakle, sastoji od niza zglo­bova i segmenata. Zglobovi su obeleženi sa , a segmenti sa 1,2, ...

Razmotrićemo neke od podela kinematičkih lanaca. Kinematičke lance mo­žemo podeliti na proste i razgranate. Prost lanac podrazumeva samo jedan niz segmenata pri čemu svaki segment ima dva zgloba, prethodni i naredni, a samo poslednji u nizu ima jedan zglob. Takvi lanci prikazani su na slici 2.6. U slučaju da prvi segment lanca nije vezan za podlogu već je slobodan (sl. 2.5) tada i taj segment ima samo jedan zglob (onaj naredni), ali to je slučaj koji za praktičnu robotiku nije bitan.

 

Razgranat lanac podrazumeva da bar jedan segment lanca nosi tri ili više zglobova (jedan prethodni i dva ili više narednih). Dakle, lanac se grana (sl. 2.7).

 

 

Sl. 2.6. Primeri manipulacionih robota sa odgovarajućim kinematičkim lancima

 

 

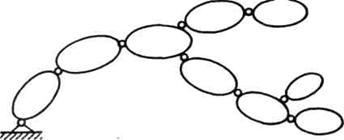
Sl. 2.7. Shema razgranatog lanca

 

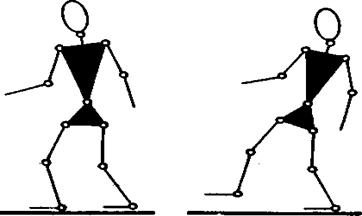
U praktičnim realizacijama robotskih sistema razgranati lanci se sreću, na primer, kod antropomorfnih hodajućih robota (sl. 2.8).

 

a)                                                                                          b)

 

Sl. 2.8. Shemu antropomorfnog hodajućeg robota

 

Po drugoj podeli kinematički lanci se dele na otvorene i zatvorene. Otvoreni lanci su oni kod kojih ne postoji zatvoreni niz, tj. iz jedne tačke lanca u drugu može se doći samo jednim putem. Primeri ovakvih lanaca su na sl. 2.6 i 2.7. Na sl. 2.8 (b) prikazan je antropomorfni hodajući mehanizam u jednooslonačkoj fazi hoda (oslonac na jednu nogu) i u toj fazi predstavlja otvoreni lanac.

 

 

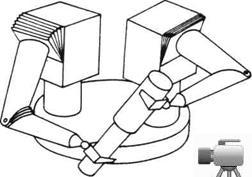
Sl. 2.9. Dvoručni manipulacioni robot

 

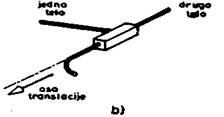
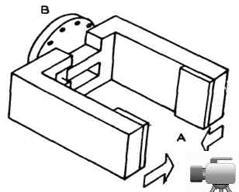
Zatvoreni lanci poseduju bar jedan zatvoreni niz segmenata i tada se iz jedne tačke tog niza u drugu može doći bar na dva načina. Praktičan primer bio bi hodajući robot u dvooslonačkoj fazi hoda (obe noge na zemlji) pri­kazan na sl. 2.8 (a), kod koga noge sa podlogom obrazuju zat­voreni niz, ili pak bilateralni(dvoručni) manipulacioni robot prika­zan na sl. 2.9.

 

Za robotske mehanizme ka­rakteristično je da tokom rada robota kinematički lanac menja svo­ju strukturu od otvorene ka zatvorenoj i obrnuto. Na sl. 2.10 pri­kazan je manipulacioni robot koji u fazi prenošenja predmeta (faza a) predstavlja otvoreni lanac, a u fazi uvlačenja predmeta u otvor (faza b) predstavlja zatvoreni lanac.  U fazi b lanac je zatvoren jer ruka sa radnim predmetom, podloga robota i zid obrazuju zatvoreni niz. Primer prikazan na ovoj slici deo je zadatka montaže.

 

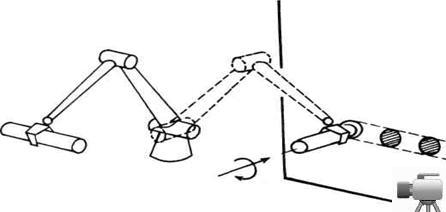
a)                                                                                b)

 

Sl. 2.10. Manipulacioni robot u zadatku montaže

 

2.1.3. Stepeni slobode kinematičkog lanca

 

Ranije smo uveli definiciju broja stepeni za jedan kinematički par. Sledeći takvu definiciju dolazimo do toga da je broj stepeni slobode zglobnog kinematičkog lanca jednak broju mogućih nezavisnih kretanja tog lanca, odnosno jednak broju nezavisnih parametara potrebnih da bi se jednoznačno odredio položaj celog lanca. Posmatraćemo kinematičke lance sa zglobovima V klase, rotacionim ili translatornim.

 

 

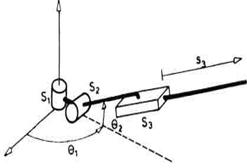
Sl. 2.11.Lanac sa  tri stepena slobode

 

Ako je u pitanju otvoreni la­nac, tada je za definisanje polo­žaja potrebno znati pomeranja u svim zglobovima lanca, dakle za koji ugao je obrnut svaki rotacioni zglob i koliki je pomeraj u sva­kom translatornom zglobu. Na­ime, kod takvih lanaca zglobovi su međusobno nezavisni i pomera-nja u zglobovima mogu biti proiz­voljna.   Na primer, kod lanca na slici 2.11 potrebno je znati uglove  i  i izduženje s3 pa takav kinematički lanac ima tri stepena slobode. Možemo zaključiti da je kod otvorenih lanaca broj stepeni slobode jednak broju zglobova.

                     

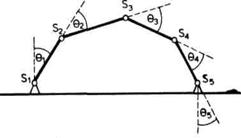
Sl. 2.12. Primer zatvorenog lanca

 

Kod zatvorenih lanaca problem je složeniji. Broj stepeni slobode lanca nije jednak broju zglobova. Posmat-rajmo mehanizam prikazan na slici 2.12. Ovaj zatvoreni lanac ima pet zglobova, svaki sa po jednim rotacio-nim stepenom slobode. Za određi­vanje položaja ovog lanca potrebno je znati uglove  i , tj. dovoljno je znati dva parametra. Dakle, lanac ima dva stepena slobode iako ima pet zglobova. Problem zatvorenih lanaca ćemo detaljnije obraditi u odeljku 4.5, u kome govorimo o kinematici i dinamici nekih klasa zatvorenih lanaca.

 

2.2.GEOMETRIJA MANIPULACIONIH ROBOTA

 

Sada ćemo sa opšte analize kinematičkih lanaca krenuti ka mehanizmima koji se javljaju u praktičnim realizacijama manipulacionih robota. Analiziraćemo strukturu "ruke" i "šake" robota. Zatim ćemo prodiskutovati broj stepeni slobode manipulacionog robota. Definisaćemo vektore koji određuju geometriju robota i na kraju pokazati postupak proračuna položaja mehanizma robota i položaja radnog predmeta.

 

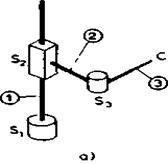
2.2.1. Minimalna konfiguracija manipulacionog robota

 

 

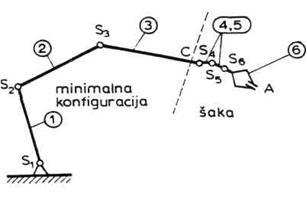
Sl. 2.13. Minimalna konfiguracija i šaka robota

 

Minimalna konfiguracija podrazumeva mehanizam sa tri zgloba, odnosno tri stepena slo­bode. Na takvu minimalnu kon­figuraciju nadovezuje se takoz­vani završni, mehanizam robota koji ćemo uslovno nazivati šaka. Na slici 2.13 shematski je pred­stavljena podela lanca na mini­malnu konfiguraciju i šaku. Sle­di da minimalna konfiguracija obuhvata zglobove S1 ,S2 i S3 i segmente 1, 2 i 3, a šaka se nadovezuje i sadrži određeni broj zglobova i segmenata (na primer 4, 5 i 6). Naziv minimalna konfiguracija potiče otuda što svaki manipulacioni robot poseduje takav mehanizam. Minimalna konfiguracija često se definiše kao mehanizam sa tri stepena slo­bode koji vrši pozicioniranje tj. dovođenje šake na željeno mesto u radnom prostoru. Kasnije ćemo videti da se pod pojmom pozicioniranja obično podrazumeva položaj samog vrha šake robota (tačka A na slici 2.13). Tako, na taj položaj, pored mini­malne konfiguracije, utiču i segmenti same šake. Otuda se može reći da minimalna konfiguracija određuje položaj korena šake, (tačka C na slici 2.13), a zajedno sa šakom vrši pozicioniranje vrha (tačka A na slici 2.13).

 

Minimalna konfiguracija je mehanizam sa tri zgloba od kojih svaki može biti rotacioni ili translatorni. Označimo sa R rotacioni, a sa T translatorni zglob. Sada možemo uvesti označavanje mehanizma na sledeći način: na primer RTT označava mehanizam sa tri zgloba (i tri stepena slobode) od kojih je prvi rotacioni, a druga dva translatorna. Sada ćemo, koristeći uvedeno označavanje obraditi najčešće sheme minimalne konfiguracije robota.

 

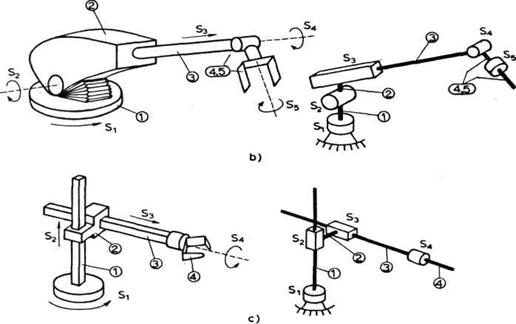
a) Pravougaona ili TTT shema. Minimalna konfiguracija pravougaone ili TTT sheme ima tri translatorna zgloba. Na slici 2.14 prikazan je primer ovakve minimalne konfiguracije i to izgled robota i njegov shematski prikaz.

 

 

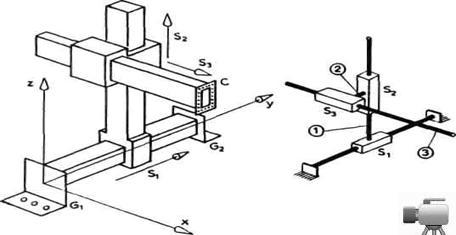
Sl 2.14. Pravougaona minimalna konfiguracija

 

Kako  je na slici prikazano, minimalna konfiguracija se završava jednom ploči­com (C na slici 2.14) na koju se zavrtnjima ili nekako drugačije vezuje šaka robota. Treba, ipak, naglasiti da minimalna konfiguracija i šaka ne moraju biti ovako odvo­jene celine. Vrlo često se i ne mogu fizički razdvojiti zato što se motori koji pokreću zglobove šake nalaze negde na segmentima minimalne konfiguracije, da bi bili bliže centralnom stubu i time manje opterećivali robot. Odatle se pogoni prenose po­godnim prenosom mehanizmom do zglobova šake. U ovakvim slučajevima podela na minimalnu konfiguraciju i šaku robota ima smisla samo shematski, a ne i na stvarnoj konstrukciji.  O načinu postavljanja motora za pogon zglobova biće više reći u kasnijim delovima knjige (glava 3).

 

Razmotrimo sada radni prostor TTT-robota ograničavajući se za sada samo na minimalnu konfiguraciju. Pod radnim prostorom minimalne konfiguracije ro­bota podrazumevamo onaj deo prostora u čiju svaku tačku može da dođe vrh konfiguracije (tačka C na sl. 2.14).

 

 

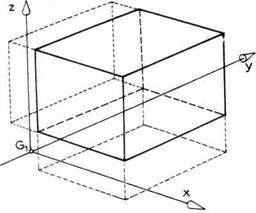
Sl. 2.15. Radni prostor pravougaone minimalne konfiguracije

 

Posmatrajmo TTT-shemu prikazanu na slici 2.14 i razmot­rimo šta je to što ograničava mo­gućnost da vrh C stigne u bilo koju tačku prostora. Ograničenje potiče otuda što pomeranje bilo kog segmenta kroz odgovarajući zglob nije ograničeno. Na pri-mer, kod klizanja zgloba S1 po šipki G1G2 uvedeni su mehanički graničnici (G1 i G2). I kod osta­lih zglobova dužina izvlačenja ili uvlačenja segmenata ograničena je samom dužinom segmenata, pa se u konstrukciji uvode graničnici. S obzirom na ovakva ograničenja, radni prostor TTT-robota bio bi pravougaonik prikazan na slici 2. 15.   Otuda i naziv pravougaona shema. Da bi bilo jasnije treba istaći da horizontalna šipka G1G2 nije segment, već predstavlja deo nepomične podloge, a segment 1 je vertikalni stub.

 

 

Sl. 2.16. Cilindrična minimalna konfiguracija

 

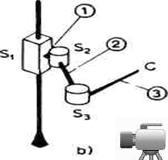
b) Cilindrična ili RTT-shema. Minimalna konfiguracija cilindrične ili RTT-sheme ima tri zgloba od kojih je prvi rotacioni, a druga dva translatorna. Na slici 2.16 prikazan je primer ovakve minimalne konfiguracije i to izgled robota i njegov shematski prikaz. Na slici 2.6 (c) prikazan je još jedan primer RTT-sheme.

 

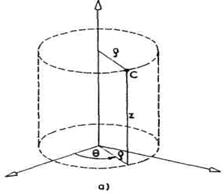
Naziv cilindrična shema potiče otuda što pomeranja u zglobovima S1, S2 i S3 tačno odgovaraju koordinatama ,z i  cilindričnog koordinatnog sistema, što se vidi upoređivanjem slike 2.16 i 2.17 (a). U daljem tekstu ćemo videti da je i radni prostor ovakvog robota cilindričan.

 

 

 

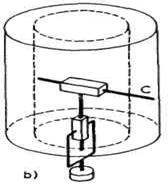
Sl. 2.17. Cilindrični koordinatni sistem i radni prostor

 

Razmotrimo sada radni prostor RTT-sheme robota. Ograničenja se ovde javljaju zbog ograničene dužine segmenta 2 i 3, te se oni mogu izvlačiti (odnosno uvlačiti) iz odgovarajućih zglobova samo do određene mere. Za obrtanje u zglobu S1 smatraćemo da nije ograničeno, mada i tu mogu da se pojave ograničenja. S obzirom na uvedena ograničenja, radni prostor cilindričnog robota izgledao bi kao na slici 2.17 (b).

 

c) Sferna ili RRT-shema,. Minimalna konfiguracija sferne ili RRT- sheme ima tri zgloba od kojih su prva dva rotaciona, a treći translatorni. Na slici 2.6 (b) prikazan je primer sfernog robota i njegova shema. Na slici 2.11 data je još jedna moguća shema sfernog robota. Treća moguća RRT- shema data je na slici 2.18 (a).

 

 

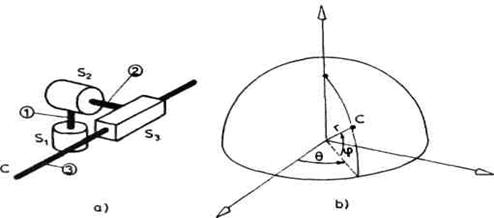
Sl. 2.18. Sferna minimalna konfiguracija

 

Pomeranja u zglobovima kod RRT-sheme približno odgovaraju koordina­tama sfernog koordinatnog sistema (slika 2.18 b), pa otuda naziv sferna shema. Primećujemo da poklapanje nije potpuno. Na shemama slika 2.18 i 2.11 vidimo da bi pomeranja u zglobovima S1, S2 i S3 odgovarala potpuno koordinatama  i r jedino ako bi dužina segmenta 2 bila jednaka nuli ili bar jako mala.

 

Razmotrimo radni prostor RRT-sheme robota. Ako uvedemo graničnike za maksimalno i minimalno izduženje u zglobu S3, a smatramo da su obrtanja u zg­lobovima S1  i S2 bez ograničenja, tada je radni prostor robota jedna šuplja lopta (slika 2.19 a). Ako postoje graničnici koji određuju krajnje tačke obrtanja u zglo­bovima S1  i S2, tada je radni prostor jedan isečak opisane lopte. Jedan primer je dat na slici 2.19 (b).

 

 

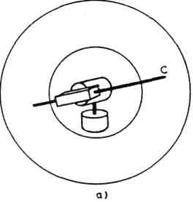
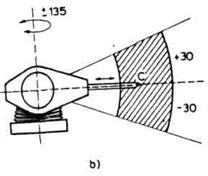
Sl. 2.19. Radni prostor sferne minimalne konfiguracije

 

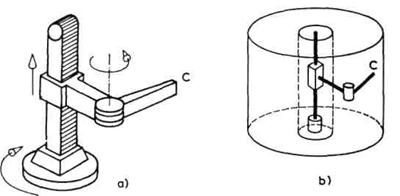
d) RTR i TRRsheme. Ove dve sheme obrađujemo zajedno zato što u onom obliku u kome se obično praktično realizuju imaju isti radni prostor. Sheme su prikazane na slici 2.20 (a), (b), a jedan konkretan primer robota na slici 2.21 (a).

 

 

 

Sl. 2.20. RTR-shema (a) i TRR-shema. (b)

 

Radni prostor RTR i TRR-sheme robota je šuplji valjak kao što je prikazano na slici 2.21 (b).

 

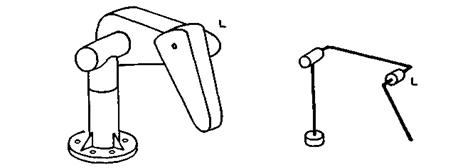
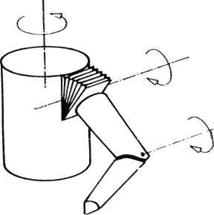
e) Laktasta ili RRR-shema Minimalna konfiguracija laktaste ili RRR- sheme ima tri rotaciona stepena slobode. Jedan primer prikazan je na slici 2.6 (a), a na slici 2.22 dat je još jedan primer.

 

Naziv laktasti robot potiče od karakterističnog "lakta" koji se uočava na ovoj shemi (L na slici 2.22). Inače, za ovu jako čestu shemu robota sreću se i drugi nazivi kao, na primer, zglavkasti ili antropoidni robot. Izdvojićemo posebno jednu od mogućih RRR-shema. Prikazana je na slici 2.23 i zbog sličnosti sa čovekovom rukom naziva se antropomorfna (čovekolika) shema.

 

 

Sl. 2.21. Primer RTR-robota i radni prostor

           

 

Sl. 2.22. Laktasti ili RRR-robot

 

Radni prostor RRR-sheme robota zavisi od mogućnosti obrtanja u svakom zglobu. Ako bi obrtanja bila bez ograničenja, onda bi radni prostor bio lopta čiji je poluprečnik određen dužinom ruke. Kako obrtanja u zglobovima nisu neograničena to će radni prostor biti jedan deo lopte složenog oblika (slika 2.24).

 

Moramo spomenuti još jedan karakterističan slučaj laktaste sheme minimalne konfiguracije. Ta shema prikazana je na slici 2.25, a zvaćemo je ASEA. Shema, po švedskom robotu marke ASEA koji je najpoznatiji. Shema je na slici prikazana u dve varijante koje se razlikuju po načinu delovanja pogonskih motora. Dejstvo pogona označeno je na slici strelicama. Za ovu shemu je karakteristično da sadrži jedan zatvoreni lanac oblika paralelograma.

 

 

                 

 

 

Sl. 2.23. Antropomorfna RRR- shema                      Sl. 2.24. Radni prostor laktastog robota

 

 

 

 

 

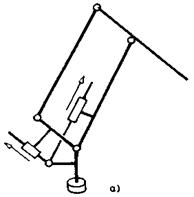
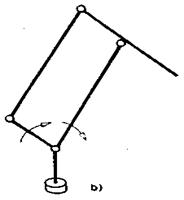
Sl. 2.25. ASEA-shema

 

2.2.2.  Završni mehanizam ili šaka robota

 

U odeljku 2.2.1 rečeno je da se mehanizam manipulacionog robota može pode-liti na dva dela: tzv. minimalnu konfiguraciju i završni mehanizam ili šaku robota (sl. 2.13). Minimalna konfiguracija dovodi šaku u željeni deo radnog prostora, od­nosno pozicionira koren šake. Razmotrimo sada strukturu završnog mehanizma ili šake robota.

 

Završni mehanizam robota sastoji se od određenog broja zglobova, a na kraju se pričvršćuje takozvani završni uređaj (engl. end-effector). Zglobovi šake su po pravilu rotacioni. Na slici 2.26 prikazana je shema mehanizma šake. Tačka C označava koren šake i tu je ucrtana pločica koja se učvršćuje za vrh minimalne konfiguracije koja je ucrtana isprekidano. Celina se može lepo sagledati ako se slika 2.26 uporedi sa slikama 2.14 i 2.16 gde su prikazane minimalne konfiguracije.

 

 

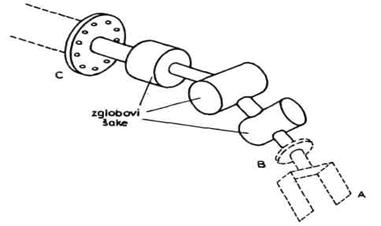
Sl. 2.26. Shema šake robota

 

Tačka B označava položaj gde se takozvani završni uređaj učvršćuje za meha­nizam šake. To je ucrtano u obliku pločice na kojoj se nalaze zavrtnji za učvršćava-nje. Završni uređaj ucrtan je isprekidano, u obliku hvataljke. Vrh završnog uređaja označen je tačkom A.

 

 

Sl. 2.27. Hvataljka robota

 

Mehanizam šake ima jedan, dva ili tri zg­loba i isto toliko stepeni slobode. Broj zglobova zavisi od namene tj. od zadatka koji će robot obavljati. S obzirom na to da minimalna kon­figuracija ima tri stepena slobode to znači da će robot ukupno imati četiri, pet ili šest ste­peni slobode. Određivanje broja stepeni slo­bode koji je potreban za obavljanje određenog zadatka je poseban problem i o tome će biti reči kasnije. Biće reči o robotima koji imaju više od šest stepeni slobode.

 

Razmotrićemo pitanje završnog uređaja robota. Opšte rečeno, u pitanju je uređaj koji neposredno izvršava zadatak koji je postavljen pred robota. Ako je postavljen zadatak prenošenja nekog predmeta tada je završni uređaj takozvana hvataljka. Obično se hvataljka crta u obliku klešta kao na slici 2.27. To je zato što su hvataljke često upravo takvog oblika. Takva hvataljka ima jedan stepen slobode, hvatanje tj. stiskanje. Pločicom B hvataljka se učvršćuje za mehanizam šake.

 

Hvataljka, međutim, ne mora da bude oblika klešta. Za neke primene pogodne su hvataljke sa vakuumskim sisaljkama kao, na primer, za prenošenje limova.

Ako se postavlja zadatak farbanja prskanjem, tada je završni uređaj pištolj za prskanje a ako je zadatak, na primer, tačkasto zavarivanje, tada je završni uređaj u obliku zavarivačkih klešta. U raznim drugim primenama pojavljuje se različiti završni uređaji. Međutim, često se koristi termin hvataljka, podrazumevajući pod tim sve vrste završnih uređaja. Pod hvataljkom se podrazumeva često i ceo posled-nji segment lanca. Na primer, u zadatku prenošenja nekog predmeta koristićemo izraz hvataljke, a podrazumevati hvataljku i radni predmet zajedno.

 

Dakle, šaka robota sastoji se od mehanizma šake (CB na slikama) i završnog uređaja, odnosno hvataljke (BA na slikama). Mehanizam šake, zajedno sa mini­malnom konfiguracijom, obezbeđuje da vrh hvataljke (A) dođe u željeni položaj i da hvataljka zauzme željenu orijentaciju u prostoru. Završni uređaj (hvataljka) neposredno izvršava postavljeni zadatak.

 

Kao što možemo videti šaka industrijskog manipulacionog robota nema mnogo sličnosti sa šakom čoveka. Međutim, treba reći da se kod eksperimentalnih protetičkih robota, a u poslednje vreme i kod industrijskih, sve češće koriste složene šake opremljene većim brojem prstiju.

 

O hvataljkama i završnim uređajima uopšte više ćemo govoriti u glavi 5 ove knjige.

 

              2.2.3. Mogućnost kretanja robota — broj stepeni slobode

 

Detaljnije ćemo analizirati mogućnost kretanja i, posebno takozvanog funk­cionalnog kretanja robota. Manipulacioni robot smo posmatrali kao otvoreni lanac bez grananja u kome su segmenti povezani zglobovima V klase koji dozvoljavaju jednu translaciju ili rotaciju. Takav mehanički sistem ima onoliko stepeni slobode koliko ima zglobova. Ako ima n zglobova, sistem će imati n stepeni slobode, bez obzira na to da li je n veće ili manje od 6. Videćemo uskoro zašto je ova vrednost 6 bitna. Dakle, robot kao mehanički sistem može da se kreće na n nezavisnih načina. Pri tome se uzimaju u obzir kretanja svih segmenata. Videćemo kasnije da je za proračun dinamike potrebno voditi računa o ovih n nezavisnih mogućnosti kretnja.

 

Sada ćemo, međutim, obratiti pažnju na kretanja koja imaju neku funkciju u ostvarenju određenog manipulacionog zadatka. Posmatrajmo mogućnost kretanja hvataljke robota, a to je poslednji segment lanca. Posmatrajmo kretanja samo jednog tela, poslednjeg u lancu, a ne celog lanca. Označimo sa nh broj stepeni slobode hvataljke u prostoru. Prvo zaključujemo da hvataljka kao telo u prostoru može imati najviše šest stepeni slobode, tri translacije i tri rotacije. Dakle, .

 

Kako hvataljka nije slobodna već lancem vezana za podlogu, to njeno kretanje može biti ograničeno ovom lančanom vezom.   Tako, za broj stepeni slobode hvataljke možemo reći da je manji ili jednak broju stepeni slobode lanca, tj.:

 

 

 

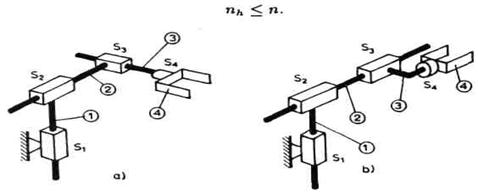
Sl. 2.28. Nesingularni i singularni mehanizam

 

Analizirajmo zašto jea ne. Ova nejednakost sugeriše da se u smislu funkcionalnog kretanja neki stepen slobode lanca može izgubiti. Najbolje je to objasniti uz nekoliko konkretnih primera. Na slici 2.28 prikazane su dve mini­malne konfiguracije TTT-tipa, a na svaku se nadovezuje šaka sa jednim zglobom, tj. jednim stepenom slobode. Svaki od ovih lanaca ima po četiri zgloba i kao me­hanički sistem ima četiri stepena slobode. Dakle n = 4. Sa stanovišta kretanja hvataljke stvari stoje drugačije. U slučaju (a) hvataljka takođe ima 4 stepena slo­bode. Tada je nh = 4, tj. nh = n i nikakvih gubitaka nema. U slučaju (b) hvataljka ima samo tri stepena slobode, tj. nh = 3 i. To je otuda što sa stanovišta kretanja hvataljke translacije S2 i S3 nisu nezavisne, već proizvode jedinstven efekat i ponašaju se kao jedna translacija. Dakle, jedan od ta dva stepena slobode se gubi. Treba reći da se o gubitku može govoriti samo sa stanovišta pomeranja hvataljke. Ako nas interesuje pomeranje celog lanca, tj. kretanje svih segmenata, tada te dve translacije ne mogu da se sjedine zbog segmenta između njih (segment broj 2) koji ima neko svoje podužno kretanje. Gubitak tj. razlika n i nh nastaje otuda što to podužno kretanje segmenta 2 ne utiče na kretanje hvataljke. Segment može kliziti kroz zglobove S2 i S3, a hvataljka i dalje mirovati.

 

Na slici 2.29. prikazana su dva nešto drugačija primera gubitka stepeni slo­bode. Lanac (a) je sastavljen od dva tela pri čemu su zglobovi S1 i S2 sferični tj. svaki dovoljava po tri relativna obrtaja tada lanac ima n = 3 + 3 = 6 stepeni slo­bode. Poslednji segment lanca (telo br. 2), međutim, imastepeni slobode jer se sa stanovišta njegovog kretanja jedan stepen slobode gubi (obrtanje tela 1 oko ose (I)).

 

  

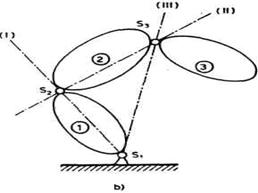
Sl. 2.29. Lanci sa sferičnim zglobovima

 

   Trosegmentni lanac sa sferičnim zglobovima (sl.2.29b) ima n=3+3+3=9 stepeni slobode. Poslednji segment, pak, ima nh = 6 stepeni slobode jer se tri stepena slobode gube (obrtanja oko osa (I), (II), i (III)).

 

a)                                              b)

 

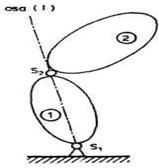
Sl. 2.30. Nesingularan i singulalaran položaj robota

 

Mehanizme kod kojih je nh < n tj. kod kojih se gube neki stepeni slobode na­zivamo singularnim mehanizmima, a one kod kojih gubitaka nema tj. nh = n nazi­vamo nesingularnim. U primeru sa slike 2.28a,b prikazana su dva mehanizma, jedan koji je stalno nesingularan i drugi koji je stalno singularan. Međutim uobičajeno je da su mehanizmi robota nesingularni, osim u nekim posebnim položajima kada postaju singularni. Posmatrajmo primer robota prikazanog na slici 2.30. Kod ovog lanca je n - 6. Kada se robot nade u položaju (a), tada njegova hvataljka može da se pomera i obrće u svim pravcima (tri translacije i tri rotacije) tj. nh  =6 = n, pa je mehanizam nesingularan. Međutim, kada je robot u položaju (b) tada hvataljka ne može da se obrće oko svoje ose (l). Dakle, nh < n i mehanizam je singularan. Treba još istaći da svaki robot čiji lanac ima više od 6 stepeni slobode (n > 6) mora uvek biti singularan, jer je . Pitanje singularnosti je važno, jer kada se nade u singularnom položaju robot svojom hvataljkom ne može napraviti one pokrete koje bi inače mogao, a koji mogu biti potrebni.

 

Analizirajmo sada mogućnost robota da obavi određene manipulacione za­datke.Definišimo prvo neke neophodne pojmove.

- Pozicioniranje podrazumeva dovođenje vrha hvataljke u željenu tačku rad­nog prostora.

 

Sl. 2.31. Potpuna orijentacija

 

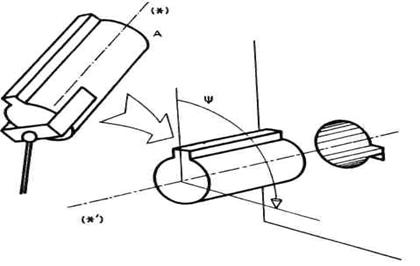
- Potpuna orijentacija hvataljke podrazumeva postavljanje hvataljke u tačno određeni uglovni položaj u prostoru. Potpuna orijentacija može se posmatrati na sledeći način. Zahteva se da se određena osa hvataljke ili radnog predmeta poklopi sa željenim pravcem u prostoru i još se zadaje ugao obrtanja hvataljke oko tog pravca. Slika 2.31 ilustruje potpunu orijentaciju. Osu predmeta (*) treba poklopiti sa pravcem otvora (*') i još predmet obrnuti oko ose za ugaoda bi se ispupčenje na bočnoj strani predmeta postavilo naspram žljeba u otvoru. Tada se tek predmet može uvesti u otvor.

 

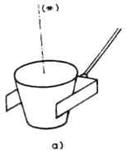
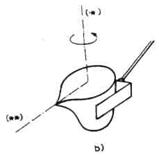
Delimična orijentacija podrazumeva samo da se određena osa hvataljke ili radnog predmeta poklopi sa željenim pravcem u prostoru.

 

Razlika između delimične i potpune orijentacije prikazana je na slici 2.32. na primeru prenošenja kontejnera sa tečnošću.U slučaju (a) važno je jedino da osa (*)bude vertikalna, odnosno u pitanju je delimična orijentacija. U slučaju (b) važna je ne samo osa (*) nego i osa (**) koja mora zauzeti željeni pravac. Kada je pravac (*) određen, onda položaj pravca (**) može biti definisan uglom obrtanja oko ose (*). U pitanju je potpuna orijentacija kontejnera.Nešto slično možemo uočiti i u zadatku prikazanom na slici 2.31. U pitanju je potpuna orijentacija zbog isturenog dela po dužini cilindra koji treba da se poklopi sa bočnim žljebom na kružnom otvoru. Kada takvog isturenog dela ne bi bilo, tj. kada bi se cilindričan predmet uvlačio u cilindričan otvor, tada bi bilo dovoljno poklopiti ose predmeta i otvora, odnosno dovoljna bi bila delimična orijentacija.

 

 

 

Sl. 2.32. Delimična i potpuna orijentacija

 

  Dakle kad govorimo o ori­jentaciji, tada razmišljamo o  jed­nom pravcu u prostoru i uglu ob­rtanja oko njega. Takav pristup je pogodan jer u praktičnom definisanju zadatka uglavnom možemo uočiti neku osu čiji je pra­vac važan u konkretnom zadatku. Dovoljno je posmatrati primere na slikama 2.31. i 2.32 i lako uočiti bitne pravce (*). Slično je sa primerima na slici 2.38.Razjasnimo   sada   pojam "vrha" hvataljke.Taj pojam podrazumeva određenu zadatu tačku hvataljke ili nekog drugog završnog uređaja.

 

To je uvek ona tačka čije je dovođenje u određeni položaj bitno u konkretnom zadatku. Na primer, pri hva­tanju predmeta bitno je pozicionirati tačku A prikazanu na slici 2.27. Kada se radni predmet uvlači u otvor bitno je pozicionirati vrh predmeta (tačka A na slici 2.31.). U slučaju farbanja prskanjem pozicionira se vrh pištolja za prskanje, a u slučaju zavarivanja vrh zavarivačkih klešta.

 

Označimo sa nz broj stepena i slobode koji je potreban za izvršenje određenog manipulacionog zadatka.

 

Za savlađivanje zadatka pozicioniranja potrebno je 3 stepena slobode tj. nz = 3.

Za savlađivanje zadatka pozicioniranja zajedno sa delimičnom orijentacijom potrebno je 3 + 2, odnosno 5 stepeni slobode (nz = 5).

Za savlađivanje zadatka pozicioniranja zajedno sa potpunom orijentacijom potrebno je 3 + 3, odnosno 6 stepeni slobode (nz = 6).

Da bi robot mogao uspešno izvršiti postavljeni zadatak potrebno je i dovoljno da bude. Obično je nh = n, a u slučaju govorimo o redundantnosti robota u odnosu na postavljeni zadatak. Dakle, redundantnost podrazumeva "višak" stepeni slobode hvataljke (nh) u odnosu na najmanji broj potreban za izvršenje zadatka (nz).

 

O višku stepeni slobode možemo govoriti i u slučaju singularnosti. Tada je n > nh, odnosno mehanizam (n) ima višak u odnosu na hvataljku (nh). I u ovom slučaju mogli bismo govoriti o redudantntosti. Međutim, ako je robot singularan samo u nekim položajima, tada izbegavamo termin redundantnosti jer mehanizam nije namerno projektovan da ima višak stepeni slobode, već je taj višak posledica smanjivanja mogućnosti kretanja hvataljke ("gubljenje" stepeni slobode) što pred­stavlja neželjenu situaciju. Ako se, pak, robot projektuje namerno tako da stalno bude singularan i da ima višak stepeni slobode, na primer, robot sa slike 2.28b, tada koristimo termin redundantni robot. Slično je sa robotima koji imaju n > 6 i koji su uvek singularni zbog  pa, dakle, i redundantni.

 

Kada je u pitanju namerna redundantnost, tad se obično radi o nekoliko ciljeva koji se žele postići. Jedan od ciljeva je postizanje velikih brzina i tada se obično projektuju tzv. paralelni stepeni slobode (sl.2.28b). Drugi cilj je izbegavanje neželjene singularnosti. Kada robot dođe u singularni položaj tj. nh trpi gubitak tada se aktivira višak stepeni slobode mehanizma čime se obično gubitak može kompenzirati. Treći cilj projektovanja redundantnih robota je stvaranje sposobnosti izbegavanja prepreka. Tada robot može da zaobiđe prepreku, a da pri tome njegova hvataljka zadrži poziciju i orijentaciju neophodnu za izvršenje zadatka. Ukupno kod svih namerno redundantnih robota problem viška stepeni slobode razrešava se uvođenjem dopunskih zahteva kojima se upošljava višak.

 

Nešto drugačiji problem javlja se kada se robot, čija hvataljka ima nh stepeni slobode, angažuje u zadatku koji se može obaviti i sa manje (dakle nz < nh). Tada se problem viška stepeni slobode rešava uvodljenjem različitih kriterijuma optimalnosti.

 

Nakon ovih definicija i diskusija o singularnosti i redundantnosti uvedimo neka ograničenja kojih ćemo se u ovoj knjizi uglavnom držati. Današnji roboti pretežno se projektuju kao nesingularni, odnosno, singularni su samo u nekim spe­cijalnim položajima. Dakle, u normalnom radu je nh = n i zato govorimo o ste-penima slobode robota ne precizirajući da li mislimo na mehanizam ili hvataljku. Ovo važi za . Tada koristimo oznaku n a podrazumevamo nh = n. Kod robota sa n > 6 stepeni slobode podrazumevaćemo nh = 6 i koristićemo termin redundanti robot. Danas se roboti uglavnom projektuju tako da imaju 4,5 ili 6 stepeni slobode. Robot sa četiri stepena slobode može da obavi pozicioniranje, za šta je potrebno tri stepena slobode, a sa preostalim četvrtim stepenom slobode vrši dopunska kretanja, što je dovoljno za izvršenje nekih jednostavnijih manipulacionih zadataka u praksi. To su obično zadaci prenošenja predmeta, opsluživanja presa i slično. Robot sa pet stepeni slobode može da izvrši zadatak pozicioniranja zajedno sa delimičnom orijentacijom. Tu spadaju, na primer, zadaci prenošenja tečnosti (sl.2.32a), jednostavniji zadaci montaže, zavarivanja i slično. Robot sa šest stepeni slobode u principu može da izvrši bilo kakav manipu-lacioni zadatak jer se on uvek može svesti na problem pozicioniranja zajedno sa potpunom orijentacijom. To su, na primer, složeniji zadaci prenošenja (sl.2.32b), montaže (sl.2.31), zavarivanja i slično.

 

2.2.4. Geometrija segmenata

 

Sada ćemo posmatrati segmente mehanizma robota i razmotriti kako se može definisati geometrija segmenata, drugačije rečeno, šta je potrebno zadati, pa da geometrija segmenata bude potpuno određena. Izložićemo dva pristupa zadavanju geometrije segmenata. Jedan potiče iz ra­dova J. Stepanjenka, a drugi je poznat kao Denavi-Hartenbergov pristup. Ovi pris­tupi se razlikuju prvenstveno po načinu postavljanja koordinatnih sistema i shodno tome načinu izražavanja vektora geometrije.

 

 

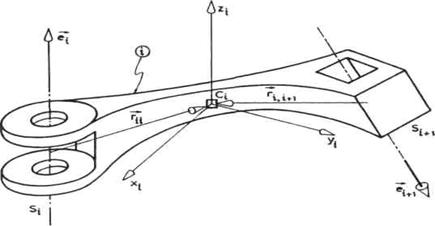
Sl. 2.33. Jedan segment mehanizma

 

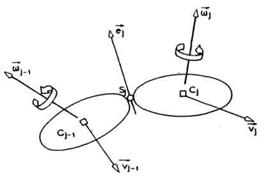
Na slici 2.33 prikazan je jedan segment mehanizma robota, na primer, i-ti segment. Zglob Si prikazan je kao rotacioni, a zglob Si+1 kao translatorni što ne mora obavezno biti nego je samo uzeto kao primer. Da bi geometrija segmenata bila potpuno određena potrebno je znati položaj koji ose zglobova zauzimaju u odnosu na segment. U slučaju na slici 2.33. radi se o osi rotacije zgloba Si i osi translacije zgloba Si+1. Takođe, neophodno je znati položaj zgloba u odnosu na težište segmenta (Ci na slici). Ose zglobova određujemo jediničnim vektorima. Pravac i pozitivni smer ose zgloba Si određeni su pravcem i smerom vektora . Isto važi i za zglob  Si+1   . Položaj težišta u odnosu na zglobove i obrnuto određujemo vektorimai prikazanim na slici. određuje položaj zgloba  Si ,apoložaj zgloba Si+1.

 

Tokom kretanja robota, položaj segmenata, a time i položaj ovih vektora, menja se u prostoru. Ali ako uočimo da se relativni položaj ovih vektora u odnosu na sam segment ne menja, onda u odnosu na sam segment, ovi vektori su nepromenljivi i predstavljaju osobinu samog segmenta. Potražimo sada način da ove "nepromenljive" veličine izrazimo. Uvedimo jedan pravougli koordinatni sistem čiji je centar u težištu segmenta, a ose sistema xi ,yi,zi vezane su za segment (sl.2.33). Položaj ovih osa može biti proizvoljan. Radi se dakle o vezanom sistemu koji se u prostoru kreće zajedno sa segmentom. Posmatrajmo sada vektor.

U odnosu na vezani sistem taj vektor je nepromenljiv pa se može izraziti trima konstantnim projekcijama , eiyi, eiti, gde je  projekcija vektorana osu xi i analogno za yi, i zi. Za ovu uređenu trojku uvedimo oznaku

 

                                                (2.1)

gde talas iznad slova označava da se radi o trima projekcijama na vezani sistem.Oznakabez talasa podrazumeva sam vektor, dakle izražen projekcijama na neki spoljašnji nepokretni koordinatni sistem (na primer, sistem vezan za pod­logu). Postupimo na isti način i sa vektorimai,i i i,i+1. Dobićemo dve trojke konstantnih projekcija

 

i,i=(ri,ixi ,ri,iyi ,ri,izi)                                           (2.2)

 

i,i+1=(ri,i+1xi ,ri,i+1yi ,ri,i+1zi)                                 (2.3)

 

i+1=( ei,i+1xi ,ei,i+1yi ,ei,i+1zi)                                (2.4)

 

Uopšte, za bilo koji vektorindeksa "i" talas iznad slova()označava tri projekcije na vezani sistem segmenata istog indeksa "i", a talas ispod slova  označava projekcije na sistem prethodnog indeksa "i -1". Rekli smo da oznake,i slične podrazumevaju uređene trojke projekcija na ose vezanog sistema.   Slično,i  i i,i podrazumevaju trojke projekcije na ose nepokretnog sistema. Tako ćemo nadalje govoriti o vektorima, a podrazumevati trojke projekcija na ose određenih koordinatnih sistema.

 

Kako je već rečeno, vektorii ,i,i i i,i+1 su konstantni vektori i predstavljaju osobinu samog segmenta. Tako, kada kažemo da treba odrediti geometriju segmenta, pod tim odrazumevamo da treba zadati ova četiri vektora. Da bi bila zadata geometrija celog lanca, odnosno robota, potrebno je za svaki segment zadati odgovarajuća četiri vektora. Potrebno je još na pogodan način definisati tip zglobova kojima su segmenti vezani. Uvodimo niz indikatora s1,s2,... ,sn i definišemo ih na sledeći način:

 

 

B. Denavi - Hartenbergov pristup

Ovaj pristup je manje opšti od predhodnog. Postavljanje osa vezanog koordinatnog sistema nije proizvoljno, već uslovljeno samom geometrijom segmenta ili preciznije položajem osa zglobova. Posmatrajmo jedan segment lanca (sl.2.34). Uobičajeno je kod ovog pristupa da numerisanje zglobova lanca kreće od nule tj. S0,S1,... .Tada u slučaju i-tog segmenta,prethodni zglob ima oznaku

Si-1,a naredni Si.

 

2.2.5 Položaj robota

 

Mehanizam robota se,po pretpostavci,sastoji od n segmenata vezanih u lanac.Kada bi segmentibili svi slobodni(nevezani međusobno) tada bi za svaki segment bilo potrebno 6 veličina da bi se odredio njegov položaj (uprošćeno rečeno, tri za položaj težišta segmenta i tri za orijentaciju), a to znači 6n veličina za ceo lanac. Međutim, kako je u pitanju lanac sa n stepeni slobode to je dovoljno zadati n veličina da bi se jednoznačno odredio položaj celog lanca. Te n veličine nazivaju se generalisane koordinate sistema. U robotici se kao generalisane koordinate usvajaju pomeranja u zglobovima mehanizma. Naime, ako zadamo geometriju mehanizma tada je dovoljno poznavati pomeranja u zglobovima da bi bio poznat položaj celog lanca (sl.2.35).

 

 

Sl.2.35. Položaj mehanizma

 

Sada ćemo dati definiciju ove generalisane koordinate preciznije. Ako ih označimo sa ql, q2,..., qn , onda je  qj generalisana koordinata koja odgovara zglobu Sj tj. to je pomeraj u zglobu. Pretpostavimo da je Sj rotacioni zglob.   Tada je indikator sj=0, a j je pomeraj u zglobu, odnosno ugao obrtanja. Ako jetranslatorni zglob, tada je indikator sj=1,  a   predstavlja translatorno pomeranje u zg­lobu.Poznavanjem indikatora  znaćemo da li vrednostpredstav­lja ugao ili translatorno pomeranje.

 

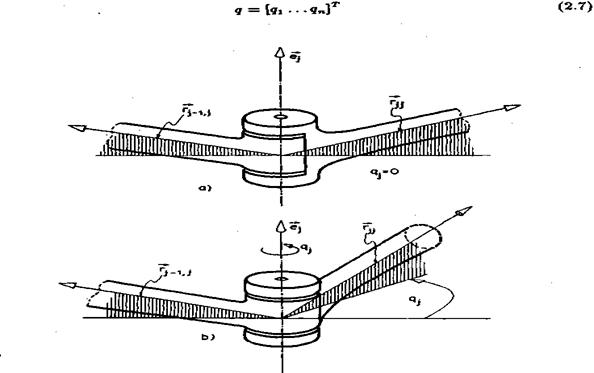
Sada ćemo posmatrati zglob i pretpostaviti da je rotacioni. Na slici 2.36 prikazana je precizna definicija ugla qj. Na slici pod (a) prikazan je ispružen zglob kada je qj=0, a na slici pod (b) prikazan je ugao qj. Dakleje ugao između negativne projekcije vektoraj-1,j i projekcije vektora j,j na ravan normalnu na osuj .Pretpostavićemo sada da je zglob Sj translatorni. Na slici 2.37 prikazana je precizna definicija pomeranja qj. "Nulta" tačka od koje se meri pomeranje (j na slici) može se nalaziti bilo gde na osi translacije. Kada se ta tačka izabere onda se na osnovu toga određuje vektorj-1,j . Koordinatu qj definisaćemo kao rastojanje  sa odgovarajućim znakom u odnosu na pozitivni smer ose.

 

Ovde je potrebno uvesti i jedan dopunski vektor .  Sa slike se vidi:

 

 

ili opštije

 

                                   

 

Za translatorni zglob je sj=1 i relacija (2.6) daje isto što i prethodni izraza za rotacioni zglob sj=0 i relacija (2.6) pokazuje da je   .

Generisane koordinate koje određuju međusobni položaj susednih segmenata nazivaju se često unutrašnjim koordinatama mehanizma robota i govori

se o unutrašnjem položaju robota. Uvedimo još n-dimenzioni vektor (kolona mat­rica) generalisanih, odnosno unutrašnjih koordinata:      

                

 

Sl. 2.36. Generalisana koordinata u rotacionom zglobu

 

Do sada smo diskutovali o položaju mehanizma robota. Razmotrimo sada definisanje položaja hvataljke robota što je ključno pitanje za izvršavanje manipulacionog zadatka. Prvo ćemo uvesti jedan spoljašnji nepokretni koordinatni sistem (vezan za podlogu) sa osama  čiji početak smeštamo u prvi zglob lanca (S1) (na slici 2.35).

 

Sada ćemo razmotriti vezu između uvedenog nepokretnog i ranije uvedenih koordinatnih sistema vezanih za segmente. Posmatrajno neki vektorkoji pred­stavlja neku karakteristiku j-tog segmenta ili zgloba. Taj vektor se može izraziti projekcijama na ose nepokretnog sistema kada se označava sa . Može se  takođe izraziti projekcijama na vezani sistem j-tog segmenta kada se označava sa

 

 

 

Sl. 2.37. Generalisana koordinata u translatornom zglobu

 

Konačno, nekada je potrebno izraziti vektor projekcijama na vezani sistem prethodnog segmenta (j-1). Tada se označava sa . Između ovih vektora postoji matrična veza. Može se naći matrica Aj dimenzija 3x3 koja zadovoljava

 

                                                (2.8)

 

i koja se naziva transformaciona ili prelazna matrica vezanog sistema j- tog seg­menta. Matrica omogućava prelaz vektora iz j-tog vezanog sistema u spoljašnji nepokretni, i obrnuto:

 

                                   (2.9)

 

Pri množenju vektora matricom, vektor se posmatra kao kolona matrica di­menzija 3x1 koja sadrži projekcije vektora. Može se takođe naći i matrica Aj-1,j  dimenzija 3x3 koja zadovoljava

 

                                      (2.10)

 

i naziva se relativnom prelaznom matricom. Ona omogućava prelaz vektora iz jednog vezanog sistema u drugi (iz j-tog u prethodni, tj. (j-1)). Obrtna transfor­macija  je

 

                               (2.11)

 

Sada treba uočiti da relativna prelazna matrica Aj-1,j zavisi samo od koordinate i može se izračunati ukoliko je zadata geometrija susednih segmenata i koordinata . Matrica Aj zavisi od svih koordinata prethodnih zglobova tj. od. Detaljno izvođenje postupka za izračunavanje prelaznih matrica dato je u prilogu Pl.

 

Korišćenjem prelaznih matrica prebacivaćemo iz sistema u sistem vektore geometrije, vektore brzina, ubrzanja, sile i sl.

 

Sada ćemo preći na analizu mogućnosti određivanja položaja završnog uređaja,odnosno hvataljke robota. U odeljku 2.2.3 već je izložena mogućnost kretanja hvataljke i rečeno je da hvataljka može imati najviše šest stepeni slobode: tri translacije i tri rotacije. Zato, da bi se odredio potpuni položaj hvataljke, potrebne su tri veličine koje će odredit i njen položaj (translacije) i tri veličine koje će definisati orijentaciju, odnosno uglovni položaj (rotacije).

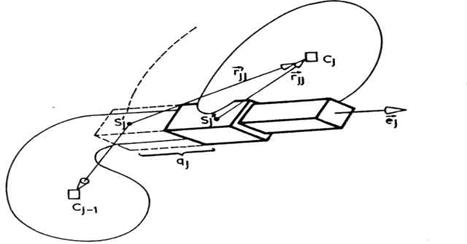
Pošto je hvataljka telo, to, kada govorimo o položaju određenom trima veliči­nama, mislimo na položaj jedne tačke tog tela. U slučaju hvataljke robota misli se po pravilu na vrh hvataljke (na ranijim slikama tačka A). Podsetićemo se da smo pod pojmom vrh hvataljke podrazumevali onu tačku završnog uređaja čije pozicioniranje je bitno u konkretnom manipulacionom zadatku.

 

Položaj vrha određujemo sa tri Dekartove koordinate: xA, yA, zA. Orijenta­ciju određujemo pomoću jednog pravca i ugla obrtanja oko tog pravca.

 

 

 

Sl. 2.38. Dva primera  zadavanja  orijentacije

 

S obzirom na to da je  pitanje pozicije tačke A jasno, razmotrićemo detaljnije pitanje orijentacije. Prvo, potrebno je da određenu zadatu osu hvataljke dovedemo u željeni položaj u prostoru. Način zadavanja ose hvataljke, odnosno pravca u od­nosu na hvataljku može biti različit. Recimo da je jedna od mogućnosti zadavanje jediničnog vektora ose izraženog u vezanom sistemu hvataljke: vektor . Uvodjenje pravca i obrtanja oko tog pravca kao načina zadavanja orijentacije veoma je prikladno za definisanje manipulacionih zadataka. Dva primera smo već videli na slikama 2.31 i 2.32, a još dva prikazana su na slici 2.38. U primeru (a) potrebno je osu zavrtnja (*) poklopiti sa osom otvora, a zatim vršiti obrtanje ψ oko tog pravca. U primeru (b) bitna je osa prosipanja i ugao ψ koji određuje zakon prosipanja.

 

Dakle, izbor pravca (*) (jediničnog vektora ) je u principu proizvoljan i on se bira tako da odgovara konkretnom manipulacionom zadatku.

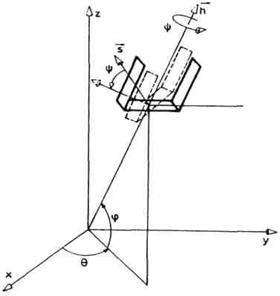
Gledano u odnosu na spoljašnji  nepomični prostor, odnosno spoljašnji koor-dinatni sistem, pravac (*) možemo definisati pomoću dva ugla θ i φ, kako je to prikazano na slici 2.39. Tako dolazimo do skupa od tri ugla θ , φ i ψ koji definišu orijentaciju. Ugao θ obično se naziva ugao pravca ili ugao skretanja, φ se naziva ugao elevacije ili ugao propinjanja, a ψ se naziva ugao valjanja.

 

 

Sl. 2.39. Uglovi orijentacije

 

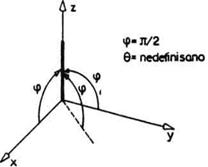
Istaknimo da ovakav način za­davanja orijentacije pomoću tri ugla može dovesti do određenih problema. Konkretno, ako je pravac (*) ver­tikalan tj. φ = , tada ugao nije moguće jednoznačno odrediti (sl. 2.40). Takve položaje nazivamo prividnim singularitetima za razliku od singulariteta koji su objašnjeni u odeljku 2.2.3. koje možemo nazvati stvarnim singularitetima jer tada ro­bot "gubi" neke stepene slobode.

 

Ukupno, položaj hvataljke (ili nekog drugog završnog uređaja) od­ređujemo sa šest parametara: xA,yA,zA , θ , φ,ψ. Ovaj broj parametara je prikladan ukoliko se hvataljka posmatra kao izolovano telo ili, pak, ako je nh = 6. Međutim, ako je nh < 6 (na primer, kod robota sa 5 stepeni slobode nh  n = 5) tih šest pa­rametara nisu nezavisni.   U slučaju nh = 5 usvajamo pet nezavisnih parametara kojima određujemo položaj. Neka su to xA,yA,zA, θ, φ.

 

Ako je nh = n, tada uvedenih šest ili pet parametara određuju i položaj celog mehanizma. Kako se ovim parametrima određuje položaj u od­nosu na spoljašnji prostor (spoljašnji sistem), to često koristimo termin spoljašnje koordinate robota.

Dakle, u slučaju nh = 6 vektor spoljašnjih koordinata je

 

                                          (2.12a)

 

a u slučaju nh = 5 vektor je

 

                                                (2.12b)

       

Ako je u pitanju robot sa manje od 5 stepeni slobode, tada se ne može govoriti o spoljašnjim koordinatama, već se govori o generalisanom vektoru položaja X koji uključuje neke spoljašnje i neke unutrašnje koordinate. Na primer, ako je nh = n = 4 tada uvodimo vektor. Dakle, rešavamo pozicioniranje i preostaje jedan stepen slobode za dopunske radnje (sl. 2.41). U prethodnom izlaganju uveli smo određivanje položaja preko unutrašnjih ko­ordinata (2.7) i preko spoljašnjih koordinata (2.12). Nameće se i logično pitanje veze ovakvih načina izražavanja. Vektor q je dimenzije n, i ako je zadat, onda je jednoznačno određen i vektor X dimenzije nh (podsećamo nh  n).   Obratni problem je složeniji. Vektor X polazi od položaja hvataljke i ako je nh < n, tada postoji beskonačno mnogo rešenja q koja zadovoljavaju zadato X. Ako je nh, = n (nesingularni robot) tad je za zadato X, vektor q ili jednoznačan ili višeznačan ali sa konačnim brojem rešenja. Na slici 2.42. prikazan je jedan slučaju jednoznačnog rešenja (a) i jedan slučaj dvoznačnog rešenja (b).

 

 

 

                  

 

 

 

 

Sl. 2.40. Prividni singularitet                           Sl. 2.41. Robot sa četiri stepena slobode

 

 

                    

 

 

Sl. 2.42. Jednoznačnost i višeznačnost rešenja unutrašnjeg položaja

 

U slučaju nh < n (singularni ili redundantni robot) problem višeznačnosti je složen i nećemo ga ovde razmatrati. Višeznačnost rešenja kod nesingularnih robota (nh = n) rešavaćemo u oblasti kinematike tako što ćemo umesto računanja koordinata q računati njihove vremenske izvode q, odnosno generalisane brzine.

 

2.3. KINEMATIKA MANIPULACIONIH ROBOTA

 

U ovom odeljku govorićemo o brzinama i ubrzanjima robota, o različitim načinima izražavanja ovih veličina i vezi između različitih načina. Posebnu pažnju obratićemo na transformaciju koordinata, odnosno preračunavanje kretanja iz unut­rašnjih u spoljašnje koordinate i obratno.

 

2.3.1. Generalisane brzine i ubrzanja

 

Kada govorimo o brzini, razmotrićemo na šta se taj pojam odnosi. Prvo, uvešćemo pojam generalisanih brzina. Kako je već u prethodnom odeljku rečeno, generalisane brzine su izvodi po vremenu generalisanih koordinata, dakle . Drugačiji naziv je unutrašnje brzine jer predstavljaju izvode pomeranja u zglobovima mehanizma, odnosno brzine relativnog pomeranja segmenata.

 

Dalje, uvodimo i pojam generalisanih ili unutrašnjih ubrzanja. To su izvodi generalisanih brzina, odnosno drugi izvodi generalisanih koordinata. Iz toga sledi da su ubrzanja .

 

Uvodimo sada, pored vektora generalisanih koordinata q, još i n-dimenzione vektore generalisanih brzina () i ubrzanja ().

 

                                                       (2.13)

 

                                                       (2.14)

 

 

2.3.2. Brzine i ubrzanja segmenata mehanizma

 

Posmatrajmo jedan segment lanca, na primer j-ti, kao telo u prostoru. Tada je stanje tog tela u nekom trenutku vremena od­ređeno njegovim položajem i br­zinom. O položaju tela govorili smo ranije, a sada ćemo razmot­riti brzinu. Potrebno je pozna­vati brzinu težišta C, i ugaonu brzinu segmenta. Označimo vek­tor brzine težišta sa , a vektor ugaone brzine sa (sl.2.43).

 

Razmotrimo mogućnost iz­ražavanja brzina i, u funk­ciji generalisanih brzina . Ugaona brzina je posledica superpozicije svih rotacija u zglobo­vima lanca, počevši od podloge pa do posmatranog segmenta "j". Posmatrajmo zglob Sk. Ako je zglob rotacioni tada je sk=0 i vektor rotacije je. S ob­zirom na to da zglob ne mora biti rotacioni, to u opštem slučaju vektor rotacije pišemo u obliku . Za translatorni zglob (sk = 1) ovaj izraz je jednak nuli. Slaganjem rotacija dobijamo

 

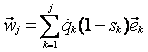                                                 (2.15)

 

što se može napisati i u rekurzivnoj formi

 

                                          (2.16)

 

Brzinu težišta  možemo takođe dobiti preko teorije vezanih vektora ili pak diferencirajući vektor položaja težišta Kako je kod lančanih sistema veoma pogodno raditi  sa rekurzivnim izrazima, to vektor položaja težišta pišemo u obliku (sl.2.43):

 

 

                    k

 

 

Diferenciranjem po vremenu dobijamo

                          (2.17)

 

pri čemu smo koristili činjenicu da je izvod nekog vektora vezanog za segment "k" jednak:, gde je ugaona brzina segmenta. Na ovaj način dobili smo izraze (2.16) i (2.17) koji predstavljaju rekurzivne izraze za brzine segmenata. Diferenciranjem po vremenu dobija se ugaono ubrzanje segmenta i ubrzanje težišta

 

                              (2.18)

 

                           k

     (2.19)

 

gde je dato relacijom (2.6).

Ako je poznato da je za nulti segment lanca tj.   podlogu mehanizma tada izrazi (2.16)-(2.19) omogućavaju da se    izračunaju postepeno, idući od prvog ka poslednjem, brzine i ubrzanja svih segmenata lanca.

 

Svi vektori koji se javljaju u ovim izrazima izraženi su u odnosu na nepokretni koordinatni sistem. Da bi došlo do primene izraza, potrebno je znati  za svaki zglob lanca. Ako je poznata geometrija lanca, tada su ovi vektori poznati ali izraženi u odnosu na vezane sisteme segmenta tj. poznato je  .Dalje, ako je poznat položaj lanca, tj. koordinate q1,...,qn tada se mogu izračunati prelazne matrice A1,...,An . Sada tražene vektore u nepokretnom sistemu možemo izračunati kao:

 

                             (2.20)

 

Ukupno, za izračunavanje svih brzina segmenata lanca potrebno je znati geometriju i položaj lanca kao i generalisanje brzineZa ubrzanje je potrebno znati još i .

 

Treba spomenuti još jednu mogućnost. Umesto izraza (2.16)-(2.19) i transfor­macija (2.20) kojima se vektori "prebacuju" u spoljašnji nepokretni sistem, moguće je zadržati vektore u vezanim sistemima i modifikovati izraze (2.16)-(2.19) tako da važe za vezane sistema. Polazeći od (2.16) i (2.17), za brzine važi

 

                                         (2.21)

 

                (2.22)

 

a analogno se iz (2.18) i (2.19) dobijaju izrazi za ubrzanja. Bez obzira na to što korišćenje izraza u vezanim sistemima omogućava veću brzinu računanja, mi ćemo, radi jasnoće, nadalje zadržati izražavanje u spoljašnjem nepokretnom sistemu. Brzine  i  moguće je predstaviti u obliku linearnih formi po generalisanim brzinama:

 

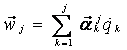                                                      (2.23)

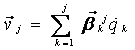                                                    (2.24)

 

(gde "j" u oznakama  i  predstavlja gornji indeks, a ne eksponent).Sada je ubrzanja  i moguće predstaviti u obliku linearnih formi po generisanjim ubrzanjima:

 

Pređimo sada na matičnu formu pisanja. U tom cilju uvedimo dogovor da za svaki vektorodgovarajuću 3x1 matricu označavamo sa a. Tada izraze (2.23)-(2.26) možemo pisati u obliku

 

                                                                      (2.27)

                                                                      (2.28)

                                                              (2.29)

                                                             (2.30)

 

gde su sledeće matrice, dimenzija 3 x n odnosno 3 x 1, čije su kolone koeficijenti linearne forme:

 

                                                       (2.31)

 

[γj]                                                                        (2.32)

 

a matrice i su

 

                                                       (2.33)

 

                                                                       (2.34)

 

Ove matrice se često pišu bez gornjeg indeksa "j" (samo) zato što se pri rekurzivnom sračunavanju samo vrše njihove izmene i dopunjavanja kako bi odgovarale novom segmentu. Razmotrimo kako se menjaju matrice  pri povećanju j. Polazeći od rekurzivnih izraza (2.16)-(2.19) može se pokazati da je u j-toj iteraciji (prelaz od j- 1 na j) potrebno izvršiti sledeće izmene i dopunjavanja matrica

 

                                                   k

                                                          (2.35)

 

                                                                         k

                                                  (2.36)

 

                        k

                               (2.37)

 

                     k

=    (2.38)

 

Formiranje matrica  moguće je dakle izvršiti rekurzivno. U svakoj iteraciji (na primer "j") lancu se dodaje novi segment. Izračunava se relativna prelazna matrica (Aj-1,j ) i apsolutna (Aj ), pa se vektori geometrije prebacuju u spoljašnjoj nepokretni sistem. Sada se primenom rekurzivnih izraza (2.35)-(2.38) formiraji matrice polazeći od

 

2.3.3. Brzina i ubrzanje hvataljke robota

 

Hvataljka robota, kako je već rečeno, predstavlja poslednji tj.n-ti segment lanca.Težište hvataljke je tada C.Ako tako posmatramo, onda brzinu težišta  i ugaonu brzinu hvataljke  možemo izračunati onako kako je prikazano u prethodnom odeljku. Dakle, brzine hvataljke izražavamo rekurzivno polazeći od brzina prethodnog (pretposlednjeg segmenta). Iato važi i za ubrzanje težištai ugaono ubrzanje .

 

Termin hvataljka koristimo za poslednji segment lanca, bez obzira na to da li je završni uređaj zaista hvataljka ili pištolj za prskanje bojom ili neki drugi uređaj. Takođe, u fazi kada prava hvataljka nosi neki radni predmet, tada pod terminom hvataljka podrazumevamo ceo taj složeni poslednji segment (tj. hvataljku zajedno sa predmetom). Podsetimo još da smo pod pojmom vrh hvataljke podrazumevali onu tačku hvataljke koja je od ključnog interesa za vršenje postavljenog manipulacionog zadatka (vidi tačku A na slikama 2.27 i 2.31).

 

 

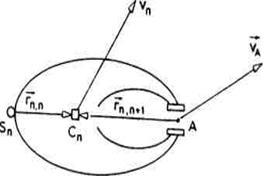
Sl. 2.44. Brzina vrha hvataljke

 

Do sada smo pokazali kako se mogu izraziti brzina i ubrzanje težišta kao i ugaona brzina i ubrzanje hvataljke robota. Međutim, za izvršenje praktičnih mani-pulacionih zadataka brzina težišta hvataljke nije od neposrednog interesa. Bitna je brzina vrha hvataljke. Ovu brzinu oz-naličemo sa i možemo je izračunati polazeći od brzine težišta (sl. 2.44).

 

Prvo je neophodno definisati polo­žaj vrha hvataljke (A) u odnosu na njeno težište (Cn). Uvedimo radi toga .Sada, pri zadavanju geometrije hvataljke zadajemo vektore i  izražene u vezanom sistemu.

 

Često se umesto  koristi oznaka da bi se dobila analogija sa prethodnim segmen­tima. Međutim, u tom slučaju se pojav­ljuje indeks n + 1 koji sugerira postojanje narednog zgloba (Sn+1), a to smatramo nezgodnim.

 

Položaj tačke A u prostoru određen je vektorom

                                        

                                                                 (2.39)

       

Diferenciranjem dobijamo brzinui ubrzanje vrha hvataljke.

 

                                       (2.40)

 

                                  (2.41)

 

U cilju primene ovih formula vektortreba izraziti u spoljašnjem sistemu:

.

Izraze za brzinu i ubrzanje vrha možemo napisati i u matričnom obliku. Pret­hodno u izrazu (2.41) uvedemo oznaku  . Sada (2.40) i (2.41) pišemo u obliku

 

                                                                 (2.42)

 

                                                          (2.43)

 

gde su vektori prevedeni u kolone matrica, označava 3x3 matricu

 

                                                      (2.44)

 

koja odgovara vektorui služi da se vektorski proizvod izrazi u matričkoj formi( ). Uvođenjem (2.27) i (2.28) u (2.42), a zatim (2.29) i (2.30) u (2.43) dobija sĺ             

                                                                                                                                               

                                                                k

 

                                        k

 

odnosno

 

                                                                        (2.45)

 

                                                              (2.46)

 

gde je

 

                                 (2.47)

 

Na ovaj način izrazili smo brzinu i ubrzanje vrha hvataljke u obliku linearne forme po generalisanim brzinama , odnosno ubrzanjima . Što se tiče ugaone brzine i ubrzanja hvataljke ostale su u važnosti formule (2.27) i (2.29) uz indeks j= n:

 

                                                                         (2.48)

                                                                 (2.49)

 

Često se izrazi (2.45) i (2.48) odnosno (2.46) i (2.49) pišu zajedno tj.

 

                                                    (2.50)

 

odnosno

 

                       (2.51)

 

Na levim stranama ovih relacija nalaze se kolona matrice dimenzije 6x1. Ove matrice brzina i ubrzanja u potpunosti određuju kretanje hvataljke. Na desnim stranama se nalaze kolona matrice q i q dimenzije nxl koje određuju kretanje celog mehanizma.Razmotrimo sada mogućnost izračunavanja jednog kretanja, u funkciji drugog. Očigledno da se kretanje hvataljke (vA,wA,wA,n) uvek može izračunati polazeći od kretanja mehanizma. Međutim obratno izračunavanje je složeniji problem i može se izvršiti samo u slučaju n = 6. Tada je matrica kvadratna i može se invertovati (podrazumevajući da je determinanta različita od nule tj. da je nh = n, pa nema singularita). Ako je n < 6 sistem je preodređen, a u slučaju n > 6 neodređen. Preodređenost tumačio tako što hvataljka ne može da se kreće proizvoljno (šestodimenziono) već kretanje treba svesti na n nezavisnih parametara (podrazumevajući nh = n). Tako dolazimo do izražavanja kretanja hvataljke preko nh = n spoljašnjih koordinata kako je već ranije definisano izrazom (2.12), tj. za n = 6 i  za n = 5. Ako je n < 5, onda uvodimo generalisani vektor položaja, npr. X = [xAyAzAq4]T.

 

2.3.4. Direktni i inverzni problem kinematike

 

Potražimo vezu između kretanja u unutrašnjim koordinatama q(t) i kretanja u spoljašnjim koordinatama X(t). Za preračunavanje q X može se uvek formirati algoritam tj:

 

X = η(q)                                                                             (2.52)

 

Međutim, inverzni postupak q = η-1(X) bio bi suviše komplikovan. Zato ćemo potražiti vezu unutrašnjih brzina (i X) kao i unutrašnjih ubrzanja ( i ). Ove veze dobijaju se diferenciranjem relacije (2.52). Tako se dobija:

 

                                                                          (2.53)

 

                                                             (2.54)

 

odnosno

 

                                                                         (2.55)

 

                                                          (2.56)

 

Matricu J = /q dimenzije nh n nazivamo Jakobijan, a matricu dimenzije nh 1 zvaćemo pridružena matrica. Jakobijeve forme (2.55) i (2.56) služe nam za preračunavanje brzina i ubrzanja. Da bi preračunavanje u oba smera bilo jednoznačno smatraćemo da je J kvadratna matrica (nh= n) i da je det J0 (nema singulariteta, ni pravih ni prividnih). Postupak formiranja Jakobijana prilično je složen problem. Pristupa njegovom, rešavanju ima više. U prilogu P2 izložen je jedan postupak kojim se izračuna­vaju Jakobijan i pridružena matrica u funkciji unutrašnjih koordinata tj. J(q) i A(). Postupak je izveden za slučaj n = 5 i n = 6, i polazi od izraza (2.51) koji se transformiše uvođenjem vektora X. Preciznije, je već deo vektora, a preostaje da se  izrazi u funkciji i i. Razmotrimo sada kako se može zadati kretanje robota. Jedna od mogućnosti je da se zada vremenska promena generalisanih (tj. unutrašnjih) koordinata, dakle q(t). Zadajemo, znaci, direktno kretanja u zglobovima mehanizma. Pošto znamo kako se tokom vremena menjaju unutrašnje koordinate q1(t),...,qn(t) jednoznačno je određeno kretanje robota. Zakonima q(t) određeni su i izvodi (t) i (t). Sada je moguće izračunati spoljašnje kretanje korišćenjem izraza (2.52), (2.55) i (2.56). Ovakvo sračunavanje spoljašnjeg kretanja X(t) ako je poznato unutrašnje kretanje q(t), nazivamo direktnim problemom kinematike robota. U nekim prostijim manipulacionim zadacima direktno se zadaju pomeranja u zglobovima. Primer za to bio bi robot na slici 2.45. Zadatak je prikazan shematski na istoj slici. Radni predmet treba preneti prvo iz tačke M0 u tačku M1 . Pri ovakvom kretanju menja se koordinata q1 za π/2. Takođe se menja koordinata q4 koja vrši obrtanje radnog predmeta za π /2. Pri kretanju od M1 do M2 menja se opet q1 unatrag za π /2 i istovremeno se menja q2 spuštajući predmet za 0,5 m. Konačno, pri kretanju od M2 do početnog položaja M0 opet se menja q2 ovog puta naviše za 0,5 m i menja se q4 koja obrće predmet unatrag za π /2 vraćajući ga tako na polazni položaj. Ovakvo zadavanje zadatka pogodno je samo za jednostavne manipulacione zadatke. U složenijim zadacima uvek je neophodno ostvariti određeno kretanje hvataljke koja će pri tome izvršiti postavljeni zadatak (vidi na primer sliku 2.38). Jasno je da je nemoguće unapred predvideti pomeranja u zglobovima (tj. q(t)) koja bi ostvarila željeno kretanje hvataljke. Zato takve zadatke određujemo preko vek­tora spoljašnjeg položaja hvataljke (vektor X). Zadaćemo kretanje vrha tako što zadajemo zakon vremenske promene koordinata xA(t), yA(t) i zA(t). Zakon pro­mene orijenatacije zadajemo tako što zadamo vremensku promenu uglovaθ(t),φ(t) i ψ(t). U slučaju robota sa pet stepeni slobode ψ (t) je zavisno i ne zadaje se.

 

 

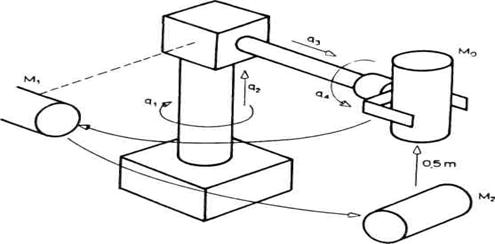
Sl. 2.45. Zadavanje kretanja  preko unutrašnjih koordinata

 

Zadali smo manipulacioni zadatak preko vremenske promene vektora X(t). Sada ćemo pokazati kako se može izračunati unturašnje kretanje q(t) ako je spoljašnje X(t) zadato. Zakon X(t) određuje i (t) i (t). Sada bi na osnovu X trebalo odrediti q, na osnovu odrediti  i konačno, na osnovu  odrediti . Međutim ovo nije lako realizovati. Već smo ranije rekli da je računanje q iz poznatog X veoma složen posao, često bez jednoznačnog rešenja. Dalje, računanje  pomoću relacije (2.55) zahteva prethodno sračunavanje Jakobijana, a njega ne možemo izračunati jer ne znamo q. Isto vazi i za pokušaj računanja  pomoću relacije (2.56).

 

Ovaj složeni problem izračunavanja unutrašnjeg kretanja q(t) iz poznatog spo­ljašnjeg kretanja X(t) naziva se inverzni problem kinematike robota. Sa nekoliko reči ćemo objasniti zašto je rešavanje ovog problema važno. Sa jedne strane, zak­ljučili smo da je manipulacioni zadatak pogodno zadati u obliku kretanja hvataljke po zakonu X(t). Sa druge strane robot se pokreće pomoću motora koji deluju u zglobovima i koji izazivaju pomeranja u zglobovima. Prema tome, za delovanje motora bitna je promena koordinata u zglobovima tj. q1(t), q2(t), ...,qn(t). Da bi se izvršila sinteza upravljanja kretanjem robota neophodno je sračunati unutrašnje kretanje q(t) odnosno rešiti inverzni problem kinematike.

 

Sada ćemo objasniti jedan praktičan postupak za numeričko rešavanje inverznog problema kinematike. Treba naglasiti da je postupak namenjen za korišćenje na računaru.

 

Pre nego što predeno na objašnjenje samoga postupka uvešćemo pojam stanja mehaničkog sistema. U strogu definiciju pojma stanja u smislu teorije sistema ovde nećemo ulaziti. Zadovoljićemo se time da kažemo da je stanje mehaničkog sistema u nekom trenutku određeno poznavanjem položaja q i brzina . Ove dve veličine (u stvari dve matrice q i ) definišu stanje zato što su položaj i brzine one veličine koje se ne mogu trenutno promeniti, već se do narednog beskonačno bliskog trenutka vremena mogu promeniti samo beskonačno malo. Za razliku od njih ubrzanje se može skokovito menjati u trenucima početka ili prestanka dejstva sile. Na ovaj način, položaj i brzine se javljaju kao neophodni početni uslovi za određivanje daljeg kretanja sistema. Zato ove veličine uzete zajedno nazivamo stanjem sistema. Pod stanjem podrazumevamo par kolona matrica, q i .

 

Analizirajmo sada početno stanje sistema koji ovde posmatramo, a to je kine-matički lanac robota. Početno stanje određeno je vrednostima q i  u početnom trenutku vremena t0, dakle q(t0) i (t0). U slučaju neredundantnih i nesingularnih mehanizama početno stanje može se definisati i preko položaja hvataljke i njene brzine u početnom trenutku t0 , dakle X(t0) i (ta). Ranije smo već na­pomenuli da ćemo zadatak zadati preko kretanja hvataljlke X(t). Na taj način biće određeno i početno stanje X(t0),(t0) . Postupak koju ćemo predložiti za rešavanje inverznog problema kinematike zahteva poznavanje početnog stanja u obliku q(t0), (t0). Za taj početni trenutak morao bi se sprovesti ranije spominjani složeni proračun unutrašnjih koordinata na osnovu poznatog položaja hvataljke X. Srećom, videćemo da se takav proračun obavlja samo jednom i to za početni trenu­tak vremena. Za kasnije trenutke vremena to neće biti potrebno. Treba još istaći da je, bez obzira na zadavanje zadataka preko kretanja hvataljke, često poznato početno stanje u obliku q(t0), (t0). To je otuda što robot obično kreće iz nekog svog uobičajenog polaznog položaja u kome su poznati svi položaji zglobova tj. sve koordinate q. Početne brzine su tada obično jednake nuli jer robot kreće iz mirovanja.

 

Sledeće što ćemo analizirati biće način numeričkog zadavanja vremenskih fun­kcija. Umesto zadavanja nekim analitičkim izrazom, što u složenijim slučajevima nije ni moguće, funkciju vremena zadajemo u vidu niza tačaka, odnosno nizom nje­nih vrednosti koje odgovaraju nizu trenutaka vremena. Primenimo ovo na slučaj zadavanja vremenske promene položaja hvataljke X(t). Sada bi za svaku kompo­nentu kolona matrice X zadali niz vrednosti koje bi definisale promenu te kom­ponente tokom vremena. Problem nastaje onda kada treba odrediti izvode (t) i (t) i kada bi trebalo izvršiti numeričko diferenciranje. Kako je numeričko dife­renciranje nepoželjan zadatak u svakom proračunu, to ćemo sada izložiti postupak kojim će se ovaj problem izbeći.

 

Poći ćemo od činjenice da početno stanje X(t0), (t0) i vremenska promena ubrzanja (t) jednoznačno određuju kretanje X(t). Zato ćemo manipulacioni za­datak i zadati preko određenog početnog stanja i vremenske promene ubrzanja. Pokažimo sada na dva primera da je zadavanje kretanja preko ubrzanja veoma pogodno. Zamislimo da želimo pravolinijsko kretanje vrha robota između dve tačke uz trougaoni profil brzine (slika 2.46al) tj. do polovine putanje (deo A0A') vrh ubrzava, a od polovine (deo A'A1) usporava tako da se u tački A1 ponovo zaustavi. Profil ubrzanja tada je prikazan na (slici 2.46bl) i može se lako zadati:

 

                                              (2.57)

 

 analogno

 

 

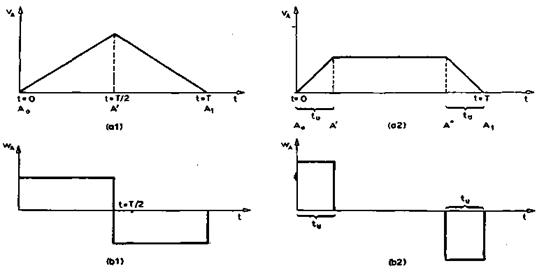
Sl. 2.46 - Trougaoni i trapezni profil brzine

 

 

odnosno 3o polovine vremena izvršenja zadatka ubrzanje je konstantno i iznosi +a, a od polovine konstantno i negativno i iznosi —a. U slučaju trapeznog profila brzine (sl. 2.46a2) razlikujemo period ubrzavanja (deo A0A'), period konstantne brzine (deo A'A") i period usporavanja (deo A"A1). Profil ubrzanja prikazan je na slici 2.46b2 i može se izraziti u obliku:

 

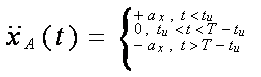                            (2.58)

 

 analogno

gde je T ukupno vreme, a tu vreme ubrzavanja, odnosno usporavanja. Treba reći da ova dva profila brzine spadaju u najčešće profile u praktičnim manipulacionim zadacima. To je važno jer vidimo da se upravo u tim najčešćim slučajevima ubrzanje zadaje veoma jednostavno (relacije 2.57 i 2.58).Kako smo već rekli da vreme i funkcije vremena posmatramo diskretno tj. u nizu trenutaka, to ćemo vremenski interval T u kome se zadatak izvršava podeliti na k podintervala Δt uvodeći vremenske trenutke t0, t1,...,tk (sl. 2.47). Sada ćemo relacije za ubrzanje (2.57) i (2.58) tretirati diskretno tj. zadati nizove vrednosti koje odgovaraju trenucima t0,t1,...,tk

 

 

Sl. 2.47 - Diskretizacija intervala kretanja

 

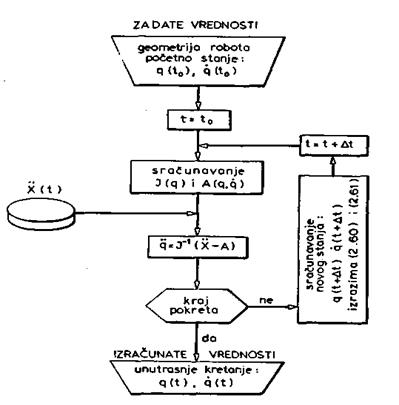
Sl. 48. Shema postupka za numeričko rešavanje inver­znog problema kinematike robota

 

Manipulacioni zadatak smatramo zadatim preko zadatog početnog stanja q(t0), (t0) i poznate vremenske promene ubrzanja hvataljke (t), Sada ćemo objas­niti postupak za rešavanje inverznog problema kinematike tj.za sračunavanje unutrašnjeg kretanja q(t). Postupak počinje sa početnim trenutkom t0 . Kako je q(t0) i (t0) poznato , to za taj trenutak možemo sračunati Jakobijan J(q) i pridruženu matricu A(q,). S obzirom na to da je (t0) poznato, sada iz relacije (2.56) izračunavamo vrednost (t0) u posmatranom trenutku t0 :

                                 

                                                                  (2.59)

 

Posmatrajmo sada subinterval između trenutka t0 i t1 . Za kratak subinterval t možemo smatrati da se q na tom subintervalu neće promeniti već će zadržati vrednost izračunatu za t0 . Tada možemo tokom  t, promenu q posmatrati kao jed­nako ubrzano kretanje i formirati izraze kojima ćemo izračunati stanje q(t1),(t1) u trenutku t1:

 

                                     (2.60)

 

                                                      (2.61)

 

Sada, kada znamo stanje q(t1), (t1) u trenutku tl počinjemo novi ciklus ponavljajući za trenutak  t1 ceo račun koji smo sprovodili za t0. Tako, rekurzivno izračunavamo stanje q, u trenucima t2, t3, ...,tk.

 

Kao rezulatat opisanog postupka dobij amo nizove vrednosti q i  koji odgo­varaju nizu trenutaka vremena, odnosno dobijamo zakon kretanja u unutrašnjim koordinatama q(t) i (t). Ovim smo rešili inverzni problem kinematike robota.

 

Ceo opisani postupak može se prikazati shemom na slici 2.48.